Integración Compleja
La magia y el poder del cálculo descansan en última instancia en el asombroso hecho de que la diferenciación y la integración son operaciones mutuamente inversas. Y, así como las funciones complejas disfrutan de notables propiedades de diferenciación que no comparten sus contrapartes reales, la sublime belleza de la integración compleja va mucho más allá de su progenitor real.
Integral de Contorno
Consideremos un contorno $C$ parametrizado por $z(t) = x(t) + i y(t)$ con $a\leq t\leq b.$ Definimos la integral de la función compleja a lo largo de $C$ como el número complejo \begin{eqnarray}\label{contour-integral} \int_C f(z)\,dz = \int_a^bf\left(z(t)\right)z'(t)\,dt. \end{eqnarray} Aquí asumiremos que $f\left(z(t)\right)$ es continua por piezas en el intervalo $a \leq t \leq b$ y nos referimos a la función $f (z)$ como continua por piezas en $C.$ Dado que $C$ es un contorno, $z'(t)$ es también continuo por piezas en $a \leq t \leq b$; y esto garantiza la existencia de la integral (\ref{contour-integral}).
El lado derecho de (\ref{contour-integral}) es una integral real ordinaria de una función compleja; es decir, si $w(t) = u(t) + i v(t),$ entonces \begin{eqnarray}\label{integral-real-cv} \int_a^b w(t)\,dt = \int_a^b u(t)\,dt + i \int_a^b v(t)\,dt. \end{eqnarray}
Ahora escribamos el integrando $$f(z)= u(x,y)+ iv(x,y)$$ en términos de sus componentes real e imaginaria, así como su diferencial $$dz=\frac{dz}{dt}dt = \left(\frac{dx}{dt}+ i \frac{dy}{dt}\right)dt = dx+ i dy$$ Entonces la integral compleja (\ref{contour-integral}) se divide en un par de integrales reales:
Ejemplo 1: Vamos a evaluar la integral $\int_C \overline{z}\, dz,$ donde $C$ está dado por las ecuaciones paramétricas $x=3t, y=t^2,$ con $-1\leq t\leq 4.$
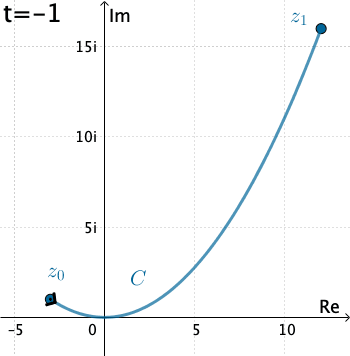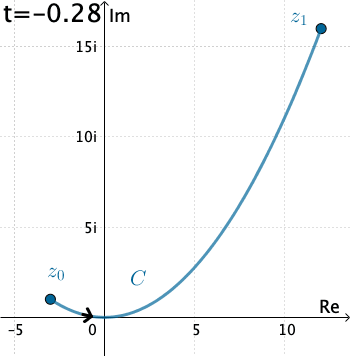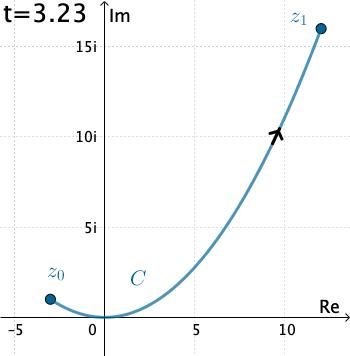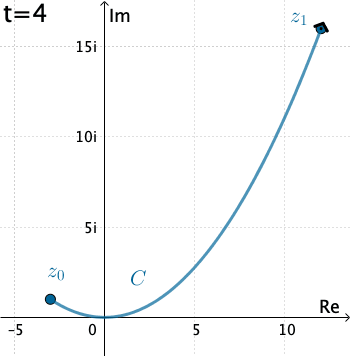
Aquí tenemos que $C$ está definido como $z(t)=3t+ it^2 .$ Por lo tanto, con la identificación $f(z)=\overline{z}$ tenemos $$f\left(z(t)\right)=\overline{3t+it^2}= 3t-it^2 .$$ Mientras que $z'(t) = 3 + 2it,$ y así la integral es \begin{eqnarray*} \int_C \overline{z}\, dz&=& \int_{-1}^4 \left(3t-it^2\right)\left(3+ 2it\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t + 3t^2i\right)dt\\ &=& \int_{-1}^4 \left(2t^3+9t \right)dt + i\int_{-1}^4 3t^2dt\\ &=& \Bigg. \left(\frac{1}{2}t^4 + \frac{9}{2} t^2\right)\Bigg|_{-1}^4 + i\Bigg. t^3\Bigg|_{-1}^4\\ &=& 195+ 65 i. \end{eqnarray*}
Ejemplo 2: Ahora evaluemos la integral $\displaystyle \int_C \dfrac{1}{z}\, dz,$ donde $C$ es el círculo $x=\cos t, y=\sin t,$ con $0\leq t\leq 2\pi .$
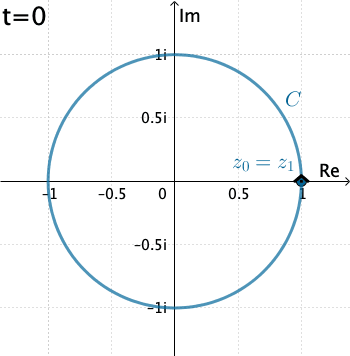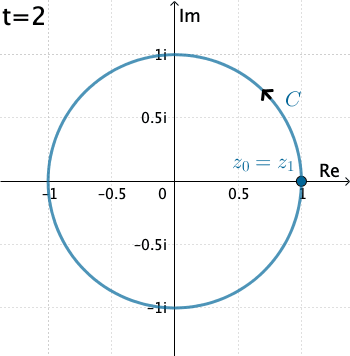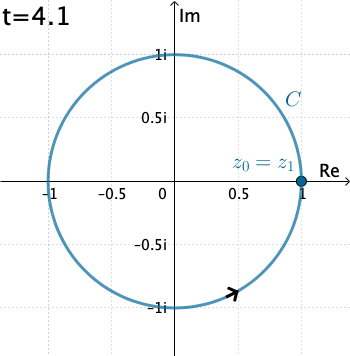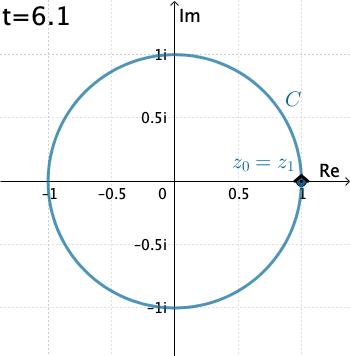
En este caso $C$ es $z(t)=\cos t + i\,\text{sen }t = e^{it}.$ Entonces $$f\left(z(t)\right)=\frac{1}{e^{it}}\quad \text{ y }\quad z'(t) = ie^{it}.$$ De esta manera \begin{eqnarray*} \int_C \dfrac{1}{z}\, dz&=& \int_{0}^{2\pi} \left(e^{-it}\right)ie^{it}dt = i \int_{0}^{2\pi} dt= 2\pi \,i. \end{eqnarray*}
Evaluación numérica de integrales complejas
Exploración 1
Usa el siguiente applet para explorar numéricamente la integral $$\int_C \overline{z}\, dz$$ con diferentes contornos $C$:
- Segmentos de línea.
- Semicírculos.
- Círculos, con orientación positiva y negativa.
También puedes cambiar la opción de domain coloring. Mueve los puntos y observa con cuidado lo que sucede. Después resuelve el Ejercicio 1 propuesto abajo.
Las flechas en los contornos indican la dirección.
- Segmento de línea: $z\left(t\right) = -2i(1-t)+ 2it,$ con $0\leq t\leq 1.$
- Semicírculo superior: $z\left(\theta\right) = 2e^{i \theta}$ con $-\frac{\pi}{2}\leq \theta \leq \frac{\pi}{2}.$
- Semicírculo inferior: $z\left(\theta\right) = -2ie^{-i \theta}$ con $0 \leq \theta \leq \pi.$
Usa el applet para confirmar tus resultados.
¿Qué conclusiones puedes deducir acerca de la función $\overline{z}$ en esta exploración?
Exploración 2
Ahora usa el applet siguiente para explorar numéricamente la integral
$$\int_C \left(z^2+z\right) dz;\qquad \int_C \frac{1}{z^2}\, dz$$
con diferentes contornos $C$ (segmentos de línea, semicírculos y círculos).
Mueve los puntos y observa con cuidad lo que sucede.
Puedes seleccionar las funciones z^2+z ó 1/z^2
de la lista en la esquina superior izquierda.
Después resuelve los Ejercicios 2 y 3.
- $C$ es un contorno desde $z_0=-1-i$ a $z_1 = 1+i.$
- $C$ es el círculo con centro $z_0$ radio $r\gt 0,$
$|z-z_0|= r$; con orientación positiva o negativa.
En este caso selecciona
Circle ↺oCircle ↻.
¿Qué conclusiones puedes deducir acerca del valor de $I_1$ y la función $z^2+z$ en esta exploración?
Ejercicio 3: Ahora considera la integral
$$I_2 =\int_C \dfrac{1}{z^2}dz.$$ Primero selecciona en el applet la función
f(z)=1/z^2.
Después analiza los valores de $I_2$ en los siguientes casos:
- $C$ es cualquier contorno desde $z_0=-i$ a $z_1 = i.$
¿Qué sucede cuando seleccionas
Line Segmenten el applet? ¿Qué sucede cuando seleccionasSemicircles? - $C$ es el círculo con centro $z_0$ y radio $r\gt 0,$
$|z-z_0|= r$; con orientación positiva o negativa.
En este caso selecciona
Circle ↺oCircle ↻. ¿Qué sucede si $z = 0$ está adento o afuera del círculo? ¿Qué sucede si $z=0$ está en el contorno, e.g. cuando $z_0=1$ y $r=1$?
¿Qué conclusiones puedes deducir acerca del valor de $I_2$ y la función $\dfrac{1}{z^2}$ en esta exploración?
Antiderivadas
Aunque el valor de una integral de contorno de una función $f (z)$ desde un punto fijo $z_0$ a otro punto fijo $z_1$ depende, en general, del camino que se toma, existen ciertas funciones cuyas integrales desde $z_0$ a $z_1$ tienen valores que son independientes del camino, como ya habrás notado en los Ejercicios 2 y 3. Estos ejemplos también ilustran el hecho de que los valores de las integrales alrededor de caminos cerrados simples son algunas veces, pero no siempre, cero. El siguiente teorema es útil para determinar cuando la integración es independiente del camino y, más aún, cuando una integral alrededor de un camino cerrado tiene un valor cero. Este es conocido como la versión compleja del Teorema Fundamental del Cálculo.
Observación: A la función $F(z)$ del Teorema 1 se le conoce como antiderivada (o primitiva).
Como consecuencia del Teorema 1 tenemos que \begin{eqnarray} \int_{C} f\left(z\right)dz=\int_{C}F^{\prime}(z) dz=0. \end{eqnarray} para todo contorno $C,$ es decir, los puntos finales son iguales.
Si la función $f(z)$ satisface la hipótesis del Teorema 1, entonces para todo contorno $C$ en el interior de $D$ que comienza en $z_1$ y termina en $z_2$ tenemos la expresión (\ref{FTC}). Por lo tanto el resultado demuestra que la integral es independiente del camino recorrido. Este hecho se ilustra en la Figura 3.
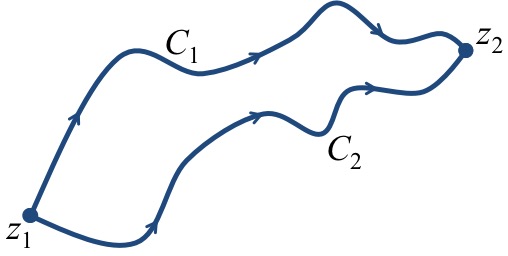
Considerando la Figura 3, tenemos que $$\int_{C_1} f\left(z\right)dz=\int_{C_2} f\left(z\right)dz$$ porque