Series
Convergencia de sucesiones
Una sucesión infinita de números complejos $\left\{z_1,z_2,z_3 \ldots\right\}$ tiene un límite $z$ si, para cada número positivo $\varepsilon,$ existe un entero positivo $n_0$ tal que \begin{eqnarray}\label{seq} \left|z_n-z\right|< \varepsilon \quad \text{siempre que}\quad n > n_0. \end{eqnarray}
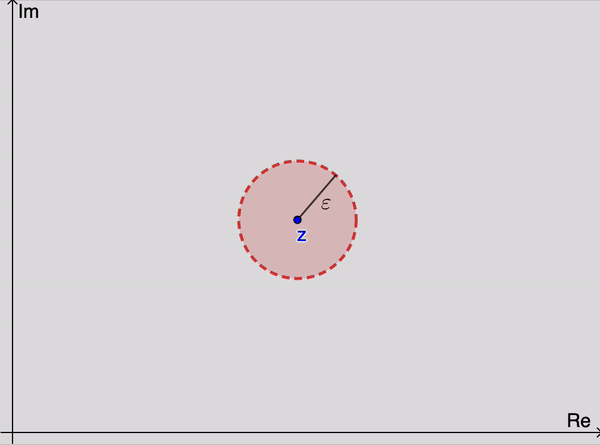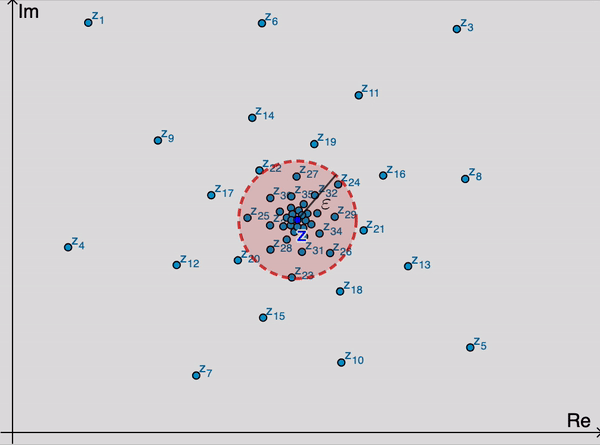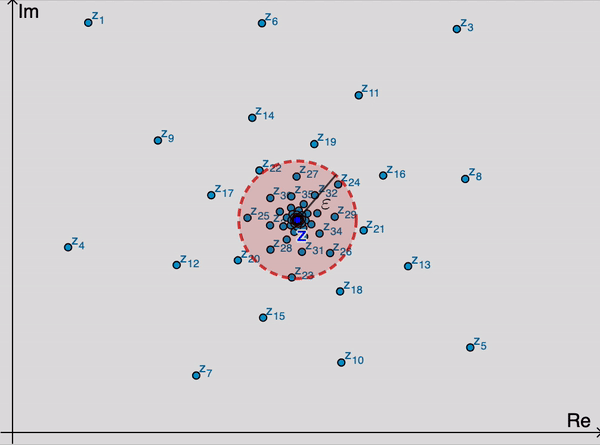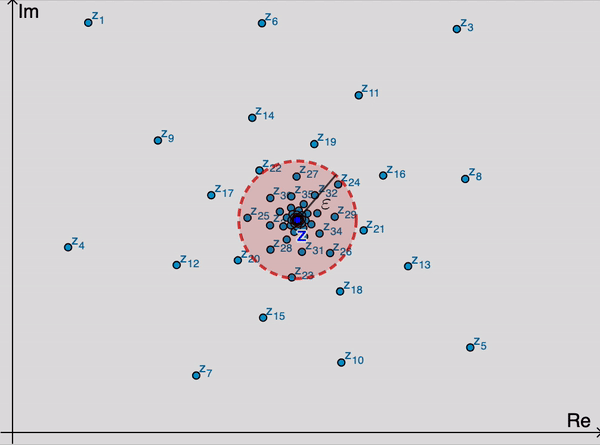
Geométricamente, esto significa que para valores suficientemente grandes de $n,$ los puntos $z_n$ se encuentran dentro de una $\varepsilon$ vecindad de $z$ (Figura 1). Dado que podemor elegir $\varepsilon$ tan pequeña como deseamos, se sigue que los puntos $z_n$ se acercan arbitrariamente a $z$ mientras su índices incrementan. Notemos que el valor de $n_0$ requerido, en general, depende del valor de $\varepsilon.$
La sucesión $\left\{z_n\right\}_{n=1}^{\infty}$ puede tener a lo más un límite. Esto es, un límite $z$ es único si existe. Cuando este límite existe, se dice que la sucecsión converge a $z$; y escribimos \begin{eqnarray*} \lim_{n\rightarrow \infty} z_n=z \end{eqnarray*} Si la sucesión no tiene límite, entonces diverge.
Demostración
Para demostrar este teorema, primero asumimos que se cumplen las condiciones (\ref{teoseq02}). Es decir, existe para cada $\varepsilon>0,$ enteros positivos $n_1$ y $n_2$ tales que \[ |x_n-x|<\frac{\varepsilon}{2}\quad \text{siempre que} \quad n>n_1 \] y \[ |y_n-y|<\frac{\varepsilon}{2}\quad \text{siempre que} \quad n>n_2. \] Por lo tanto so $n_0$ es el mayor de los dos enteros $n_1$ y $n_2,$ \[ |x_n-x|<\frac{\varepsilon}{2}\quad \text{y} \quad |y_n-y|<\frac{\varepsilon}{2} \quad \text{simpre que} \quad n > n_0. \] Dado que \[ |(x_n+iy_n)-(x+iy)|=|(x_n-x)+(y_n-y)|\leq |x_n-x|+|y_n-y|, \] entonces \[ |z_n-z|< \frac{\varepsilon}{2}+\frac{\varepsilon}{2} \quad \text{siempre que} \quad n > n_0. \] Por lo tanto se cumple la condición (\ref{teoseq01}).
En cambio, si comenzamos con la condición (\ref{teoseq01}), sabemos que para cada número positivo $\varepsilon,$ existe un entero positivo $n_0$ tal que \[ |(x_n+iy_n)-(x+iy)|<\varepsilon \quad \text{siempre que} \quad n>n_0. \] Sin embargo \[ |x_n-x|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)| \] y \[ |y_n-y|\leq |(x_n-x)+(y_n-y)|=|(x_n+iy_n)-(x+iy)|. \] Consecuentemente \[ |x_n-x|<\varepsilon \quad \text{y} \quad |y_n-y|<\varepsilon \quad \text{siempre que} \quad n > n_0. \] Por lo tanto, se satisfacen las condiciones (\ref{teoseq02}) $\blacksquare$
Convergencia de series
Una serie infinita \begin{eqnarray}\label{series01} \sum_{n=1}^{\infty}z_n=z_1+z_2+z_3+\cdots \end{eqnarray} de números complejos converge a la suma $S$ si la sucesión
Demostración
Para demostrar este teorema, primero escribimos las sumas parciales (\ref{partialsum}) como \begin{eqnarray}\label{teo03} S_N = X_N+iY_N, \end{eqnarray} donde \[ X_N = \sum_{n=1}^{N}x_n \quad \text{y}\quad Y_N = \sum_{n=1}^{N}y_n. \] Ahora el enunciado (\ref{teo01}) es verdadero si y sólo si \begin{eqnarray}\label{teo04} \lim_{N\rightarrow \infty} S_N = S; \end{eqnarray} y, en vista de la relación (\ref{teo03}) y el Teorema 1, el límite (\ref{teo04}) existe si y sólo si \begin{eqnarray}\label{teo05} \lim_{N\rightarrow \infty} X_N=X\quad \text{y}\quad \lim_{N\rightarrow \infty} Y_N=Y. \end{eqnarray} Por lo tanto, los límites (\ref{teo05}) implican (\ref{teo01}), y viceversa. Dado que $X_N=X$ y $Y_N=Y$ son sumas parciales de las series (\ref{teo02}), el teorema queda demostrado. $\blacksquare$
Este teorema es de bastante utilidad para demostrar un número de propiedades familiares de cursos de cálculo que también se cumplen con números complejos.
Propiedad 1: Si una serie de números complejos converge, el $n$-ésimo término converge a cero cuando $n$ tiende a infinito.
De la Propiedad 1 se sigue que los términos de una serie convergente están acotados. Esto es, cuando la serie (\ref{series01}) converge, existe una constante positiva $M$ tal que $$|z_n| \leq M \; \text{ para cada entero positivo } n.$$Otra propiedad importante de series de números complejos que proviene de los cursos de cálculo es la siguiente.
Propiedad 2: La convergencia absoluta de una serie de números complejos implica la convergencia de esa serie.
Recordemos que la serie (\ref{series01}) es absolutamente convergente si la serie \begin{eqnarray*}\label{series02} \sum_{n=1}^{\infty}|z_n|=\sum_{n=1}^{\infty}\sqrt{x^2_n+y^2_n}\quad \quad(z_n=x_n+iy_n) \end{eqnarray*} de números reales $\sqrt{x^2_n+y^2_n}$ converge.
Para establecer el hecho de que la suma de una serie es un número $S,$ es conveniente definir el residuo $\rho_N$ después de $N$ términos, usando las sumas parciales: \begin{eqnarray*}\label{series03} \rho_N=S-S_N \end{eqnarray*} De esta forma $S=S_N+\rho_N.$ Ahora, dado que $|S_N-S|=|\rho_N-0|,$ entonces una serie converge a un número $S$ si y sólo si la sucesión de residuos tiende a cero.
Ejemplo: Con la ayuda de los residuos, es fácil verificar que \begin{eqnarray*} \sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{whenever}\quad |z|< 1 \end{eqnarray*} Para esto necesitamos recordad la identidad $$1+z+z^2+\cdots+z^n=\frac{1-z^{n+1}}{1-z}$$ para escribir las sumas parciales
Exploración geométrica de la serie geométrica
La serie introducida en el ejemplo anterior \begin{eqnarray*} \sum_{n=0}^{\infty}z^n=\frac{1}{1-z}\quad\text{siempre que}\quad |z|< 1 \end{eqnarray*} es conocida como la serie geométrica.
Usa el siguiente applet para explorar esta serie. Arrastra el punto $ z $ alrededor. Observa lo que pasa cuando está adentro, afuera o en la frontera del círculo unitario. Arrastra el control deslizante para mostrar la suma parcial.
Code
Puedes usar el siguiente script en GeoGebra
para explorar tú mismo y hacer tu propia versión. El símbolo # indica comentarios.
#Número complejo
Z = 0.72 + ί * 0.61
#Círculo de radio 1
c = Circle((0,0), 1)
#Número de términos de la serie parcial
n = Slider(0, 250, 1, 1, 150, false, true, false, false)
SetValue(n, 250)
#Define la sucesión z^n
S = Join({0 + ί * 0, 1 + ί * 0}, Sequence(Z^j, j, 1, n))
#Define la suma parcial
SP = Sequence(Sum(S, j), j, 1, n + 2)
#Finalmente une los puntos de la suma parcial con segmentos
L = Sequence(Segment(Element(SP, j), Element(SP, j + 1)), j, 1, n + 1)
