Superficies Analíticas
Una breve historia
Un concepto tradicional para visualizar funciones complejas es el de superficie analítica. Probablemente introducido por Edmond Maillet en 1903, el cual representa la gráfica del valor absoluto de una función.
En la primera mitad del siglo XX, las superficies analíticas se hicieron bastante populares. La Figura 1 reproduce una ilustración histórica del libro Funktionentafeln mit Formeln und Kurven escrito por Jahnke y Emde y publicado en 1909. En esta imagen se muestra la superficie analítica de la función compleja Gamma y alcanzó un estatus casi icónico. ¡Hoy en día es difícil creer que esta imagen detallada dibujada a mano pueda crearse sin la ayuda de las computadoras!
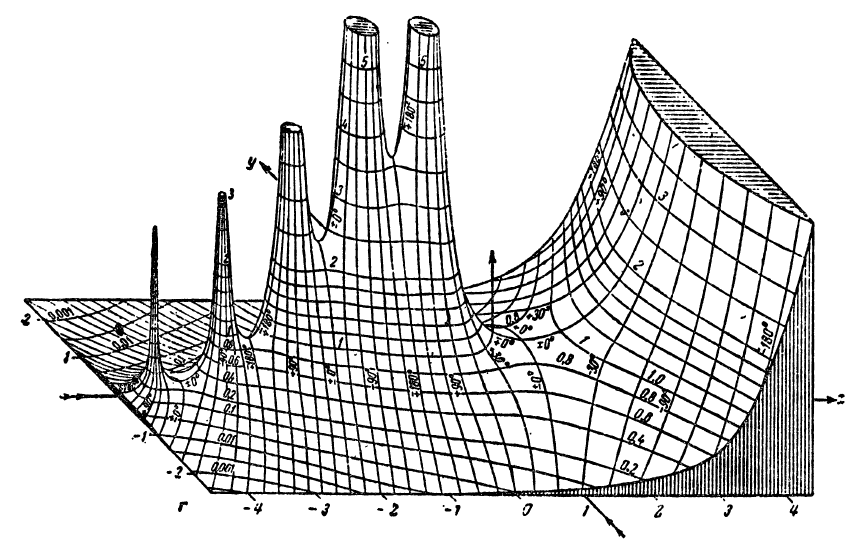
En la era de las ilustraciones en blanco y negro, esta deficiencia a menudo se compensaba dotando a la superficie analítica de líneas curvas de argumento constante como en la figura anterior, donde el argumento se indica explícitamente por su valor numérico. La tecnología informática moderna nos permite lograr el mismo efecto mucho mejor utilizando colores, lo que produce una superficie analítica coloreada como la que se muestra en la Figura 2.
Exploración Dinámica
Las funciones complejas $ f:\mathbb{C}\to\mathbb{C} $ se pueden visualizar al graficar la función $g: \mathbb{R^2} \to \mathbb{R}$ con $$g(x,y) = |f\left(x + i y\right)|.$$ El color de cada punto $\left(x, y, g(x,y)\right)$ indica la fase (o argument) del número complejo $f(x + i y).$
En el siguiente applet puedes explorar superficies analíticas coloreadas. Usa el deslizador con punto azul del lado derecho para acercar o alejar. El deslizador con el punto blanco define un escalar a $ \in [ -0.14, 1.14].$
En la práctica, a menudo es difícil generar superficies analíticas que nos permitan leer las propiedades de la función compleja de manera fácil y precisa. Un enfoque alternativo no solo es más simple sino incluso más general: en lugar de dibujar un gráfico en $\mathbb R^3,$ podemos representar una función directamente en su dominio codificando con colores sus valores por completo. Este método se llama dominio coloreado.
Nota: El último applet fue escrito por Aaron Montag usando CindyJS. El código fuente se puede encontrar en GitHub.