Cảnh quan Giải tích

Lịch sử ngắn gọn

Một khái niệm truyền thống để hình dung các hàm phức (complex functions) là cái gọi là (analytic landscapes) cảnh quan giải tích. Có lẽ được giới thiệu bởi Edmond Maillet vào năm 1903, nó mô tả đồ thị của giá trị tuyệt đối của một hàm.

Trong nửa đầu thế kỷ trước, cảnh quan giải tích trở nên khá phổ biến. Hình 1 tái hiện một minh họa lịch sử từ cuốn sách Funktionentafeln mit Formeln und Kurven của Jahnke và Emde năm 1909. Nó cho thấy cảnh quan giải tích của hàm Gamma phức và đạt được một địa vị gần như mang tính biểu tượng. Ngày nay thật khó tin rằng bức tranh chi tiết được vẽ bằng tay này có thể được tạo ra mà không cần sự trợ giúp của máy tính!

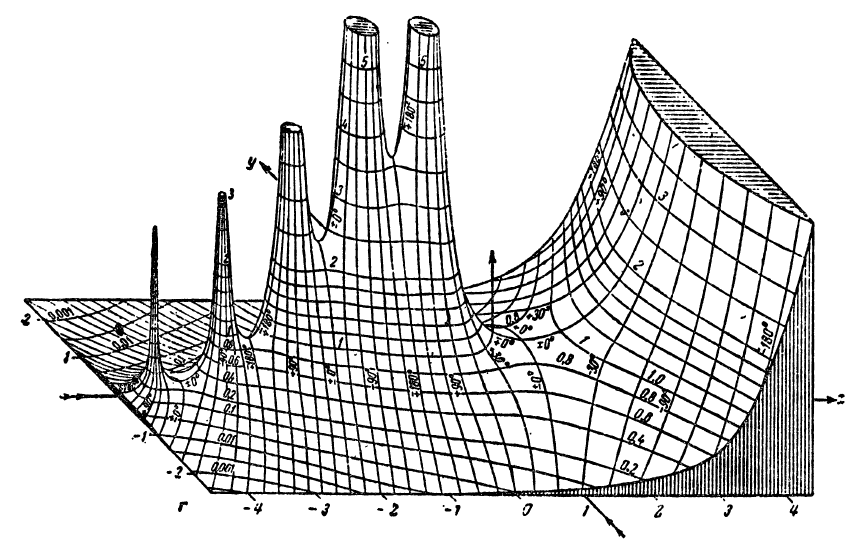
Trong thời đại của các hình minh họa đen trắng, khuyết điểm này thường được bù đắp bằng cách trang bị cho cảnh quan giải tích các đường có argument không đổi như trong hình trước, nơi argument được chỉ ra một cách rõ ràng bằng giá trị số của nó. Công nghệ máy tính hiện đại cho phép chúng ta đạt được hiệu quả tương tự tốt hơn nhiều khi sử dụng màu sắc, tạo ra cảnh quan giải tích có màu được hiển thị trong Hình 2.

Cảnh quan giải tích có màu của $\Gamma(z).$ Nhấp vào đây để mở trong cửa sổ riêng biệt.

Khám phá động

Các hàm phức $ f:\mathbb{C}\to\mathbb{C} $ có thể được hình dung bằng cách vẽ đồ thị hàm $g: \mathbb{R^2} \to \mathbb{R}$ với $$g(x,y) = |f\left(x + i y\right)|.$$ Màu sắc của mỗi điểm $\left(x, \,y, \,g(x,y)\right)$ chỉ ra pha (hoặc argument) của số phức $f(x + i y).$

Trong ứng dụng dưới đây, bạn có thể khám phá các cảnh quan giải tích có màu. Sử dụng thanh trượt màu xanh ở bên phải để phóng to/thu nhỏ. Thanh trượt màu đen xác định một scalar thực a $ \in [ -0.14, 1.14].$

Chọn một hàm f(z) từ danh sách sau:

Trong thực tế, thường rất khó để tạo ra các cảnh quan giải tích cho phép chúng ta đọc các tính chất của hàm phức một cách dễ dàng và chính xác. Một cách tiếp cận thay thế không chỉ đơn giản hơn mà còn tổng quát hơn: Thay vì vẽ đồ thị trong $\mathbb R^3,$ chúng ta có thể mô tả một hàm trực tiếp trên miền của nó bằng cách mã hóa màu cho các giá trị của nó một cách hoàn toàn. Phương pháp này được gọi là (domain coloring) tô màu miền.

Ghi chú: Ứng dụng cuối cùng được viết bởi Aaron Montag sử dụng CindyJS. Mã nguồn có thể được tìm thấy tại GitHub.