Ứng dụng của
(Conformal mappings) Ánh xạ Bảo giác

(Hydrodynamics) Thủy động lực học

Nếu chúng ta có một chất lỏng không nén được, không nhớt (ở trạng thái ổn định), chúng ta quan tâm đến việc tìm trường vận tốc của nó $$\mathbf V (x,y)= \left(u(x,y), v(x,y)\right).$$ Từ giải tích vector, chúng ta biết rằng 'không nén được' có nghĩa là độ phân kỳ $\text{div}\,\mathbf V =0.$ (Chúng ta nói $\mathbf V$ là không có phân kỳ (divergence free).) Chúng ta giả định rằng $\mathbf V$ cũng là một dòng thế (potential flow) và do đó không có tuần hoàn; tức là $\mathbf V = \text{grad } \phi $ với $\phi$ nào đó được gọi là thế vận tốc. Do đó $\phi$ là điều hòa vì $$\nabla^2\phi = \text{div } \text{grad }\phi = \text{div } \mathbf V=0.$$ Vì vậy khi chúng ta giải $\phi$, chúng ta có thể thu được $\mathbf V$ bằng cách lấy $\mathbf V = \text{grad } \phi$. Tức là \begin{eqnarray*} u=\frac{\partial \phi }{\partial x},\quad v=\frac{\partial \phi }{\partial y}. \end{eqnarray*}

Liên hợp $\psi$ của hàm điều hòa $\phi$ (sẽ tồn tại trên bất kỳ miền liên thông đơn nào) được gọi là (stream function) hàm dòng, và hàm giải tích $$F=\phi +i\psi$$ được gọi là thế phức (complex potential).

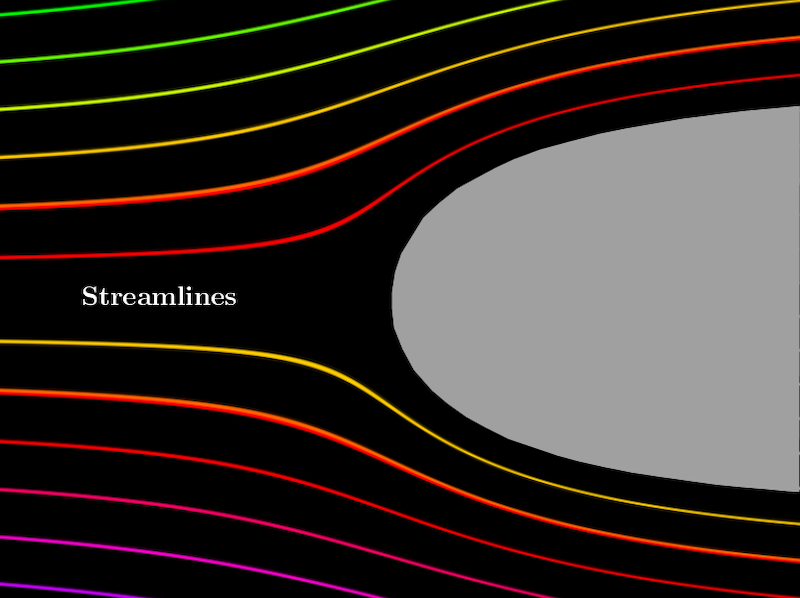
Hàm dòng (Stream function) phải thỏa mãn \begin{eqnarray*} u=\frac{\partial \psi }{\partial y},\quad v=-\frac{\partial \psi }{\partial x}. \end{eqnarray*} Cuối cùng, các đường $\psi$ không đổi có $\mathbf V$ làm tiếp tuyến của chúng, vì vậy các đường $\psi$ không đổi có thể được hiểu là các đường mà dọc theo đó các hạt chất lỏng chuyển động; do đó có tên gọi hàm dòng (stream function).